↑[画像A]曲線は円の一部。斜めに延びる濃い灰色の線は今回は使いません^q^
Bve5ではレールから成る線路など、目に見える物をストラクチャと呼びます。ストラクチャの配置には、自分の走行する線路である自線を基準として、自線からnメートルの位置にとあるストラクチャを置くという形を取ります。
自線の線路ストラクチャであれば、大抵は自線からx軸方向0mの位置に置く、とマップファイルに書いています。
ところで、現実の路線では線路は永遠に1本だけということは無く、どこかでもう1本以上の線路が自線から分岐または合流するはずです。
この分岐して自線から遠ざかっていく線路ストラクチャの配置を自線からの位置と角度を計算して配置していくなどでも可能ですが、Bveでは他線というものが用意されています。
Trackから始まる構文が他線の線形に関わる構文です。
この他線も自線からx軸方向何メートルの位置に他線を引くという形を取ります。他線へのストラクチャ配置は、今度は、ある他線からnメートルの位置に、とあるストラクチャを置くという形を取ります。
このように、他線を基準としたストラクチャの配置が他線によって可能になります。
これを自線から見れば、自線から左右xメートルの位置に引いた他線から左右nメートルの位置にストラクチャを配置するということになります。
なぜこんなことをまず書いているのかというと、とまりがまだ小学校の中学年だったBve2時代、この概念を理解するのに多少の時間が必要だったという記憶が十数年経ってもあるからです^q^;
自線が直進したまま、他線が曲線半径R=400[m]で左へ離れていく…こんなシチュエーションのとき、他線座標の計算が必要になります。
Bveでは自線の場合、カーブのある区間はCurve構文で実現できますが、一方で他線の場合は、Position構文とInterpolate構文があるだけです。
これらには他線曲線補間というオプションもありますが、ここに400と入力しただけでは上の状況を作れません。曲線の始点と終点における、自線からの距離も入れて機能するものなのです。
そんなわけで、R400の曲線が進行方向に100m続いたら、曲線の終点では自線から一体何メートル離れるのかを計算しなければなりません。
自線が曲線のときの計算法は別の機会にして、自線は直進したままの場合で計算していきます。
なんかライトノベルのタイトルみたいになってしまった^q^
自線が直線のまま、他線が曲線半径Rの曲線を描くとき、どのように考えれば自線と他線との距離がでるでしょうか。

↑[画像A]曲線は円の一部。斜めに延びる濃い灰色の線は今回は使いません^q^
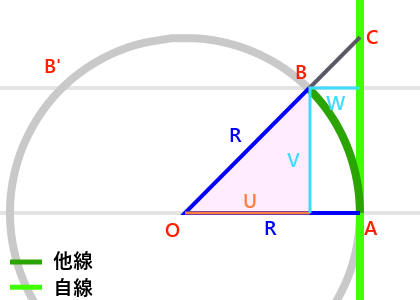
他線の曲線の始点Aから終点Bまである曲線をどんどん延ばしていくと最終的には点Oを中心とした円が描けます。ということは、他線の座標計算は円の座標を計算すればいいということになります。円の公式を使えばいいのですが、とまりは数学適性がマイナスに触れているので、図を書いてごり押していきます。曲線の始点を自線から始めるとすると点Aのx座標は0です。そして、曲線の終点Bのx座標がわかればBve上で綺麗な曲線が引けます。
曲線の終点Bのx座標は、水色の横線Wの長さを求めれば出てきます。円の中心Oと曲線の始点Aを結んだ線分OAに注目すると、線分OAは曲線半径Rの長さに等しく、さらに水色の横線Wの長さとオレンジの線Uの長さを足したものとも等しいことがわかります。
つまり、水色の横線Wの長さは曲線半径Rからオレンジの線Uの長さを引けば出せます。
ここで、点Bから垂直に線分OAまで降ろした点と点O、点Bを結ぶと直角三角形が見えてきます。[画像A]で薄い桃色をしている部分です。OB間の線の長さは曲線半径Rで、点Bと点Bから垂直に線分OAまで降ろした点とを結んだ線の長さは水色の線Vと同じ長さです。
そして、線Vの長さは[画像A]の通り、曲線の終点から始点までの距離程と同じです。
オレンジの線Uの長さがわかれば水色の線Wの長さもわかります。
これを求めるためには薄い桃色の部分が直角三角形であり、3辺の内、2辺がわかっていることから、三平方の定理とも呼ばれる、ピタゴラスの定理を使うことによって、オレンジの線Uの長さを求めることができます。
ピタゴラスの定理とは、直角三角形において、斜辺の2乗と、その他の2辺をそれぞれ2乗して足した値は等しくなるというものです。
というわけで、式は、
曲線半径R(斜辺)^2 = U^2 + V^2
となります。Uがわからないので、Uについて解く式に直します。
U^2 = R^2 - V^2
このままだとUの2乗した数が出るのでルートをとって、
U =± √(R^2 - V^2)
数値が2つ出てきましたが、これはあとで説明します^q^
仕上げです。[画像A]のとおり、曲線半径Rからオレンジの線Uを引いてWが出ます。点Bのx座標をpとして、
p = ∓R ±√(R^2 - V^2)
このように値が4つも出てきます。
なぜ4つも出てくるのかというと、[画像A]の通り、曲線の終点B地点と同じy座標を持つ点Bʹの数字が出るためです。さらに曲線半径Rが正でも負でも2乗すれば同じ数が出てきます。つまり、この円は自線を挟んで反対側にも表れるということです。
値が4つも出てきたので条件を付けて整理します。
他線の曲線が曲線半径Rで右にカーブする場合、つまりR>0のとき、
p = R - √(R^2 - V^2)
他線の曲線が曲線半径Rで左にカーブする場合、つまりR<0のとき、
p = -R + √(R^2 - V^2)
さて、これらを使って、他線が自線上からR600で右に100mだけカーブを描いて分岐するとき、カーブが終わる100m先では他線は自線からどれだけ離れているのか計算してみます。
式の記号にあてはめると、R=600,V=100です。
p = 600 - √(600^2 - 100^2)
p = 8.392…
というわけで、他線は約8.4m自線と離れることがわかりました。
他線の曲線終点からそのまま他線を直進させると、自線からはどのくらいの角度で離れていくのか、角度をラジアン(弧度)で求めてみます。弧度法のラジアンと度数法の角度との関係は180[deg] = pi(円周率)[rad]になります。ここでは、度数法の度(°)は[deg(degree)]、弧度法のラジアンは[rad(radian)]と略します。
角Bの外角は、角Bをのぞいた2つの内角の和です。2つの内角の内1つは直角三角形の直角です。円の接線は半径に対して垂直になるので、角Oが他線と自線の離れ具合を表します。
というわけで角Oの角度を求めます。コサインを使っても、サインでもタンジェントでも角Oは求まりますが、半径Rと線Vが最初からわかっている数値なのでサインを使います。
直角三角形によるsinの定義から、
sin角O = 線V / 半径R
これで出てきたcos角Oの値から三角関数表を使って角度に変換してもいいのですが、PCであれば三角関数の逆関数である逆三角関数を使えば簡単です。
arksin角O = V / R
ここで出てくる値はラジアン(rad)なので度(deg)に変換したい場合は180 / pi(円周率)を掛ければ出せます。
他線が自線上からR600で右に100mだけカーブを描いて分岐するとき、カーブの終点では他線は自線とどの程度の角度が付いているのか計算してみます。
sinθ = 100 / 600
sinθ = 0.16666…
これはあくまでもsinの数値なので逆三角関数を使って、
arkcos(0.16666…) = 0.16745…[rad]
他線が自線上からR600で右に100mだけカーブを描いて分岐して、そこからさらに25m直進するとき、他線は自線からどのくらい離れているかを計算してみます。
角度の付いた直線部分の離れ具合の計算についてはもう完全に直角三角形なので、直進距離 * tan(rad)で求まります。
よって、
25 * tan(0.16745) = 4.22577…
というわけで、カーブ終点では約8.4m自線から離れて、さらにそこから25m先まで他線が直進したとすると、さらに4.2m離れることがわかりました。
Bve5の他線構文にすると、
Distance; Track[1].X.Interpolate(0, 600);
Distance + 100; Track[1].X.Interpolate(8.4, 0);
Distance + 25; Track[1].X.Interpolate(8.4 + 4.2, 0);
となります。